Как посчитать процент от числа при расчёте налогов, кредитов и вкладов

Понятие «проценты» известно всем, впервые о них говорили в школе. Учителя показывали примеры счета и рассказывали, зачем требуются проценты. Однако на практике бывает сложно представить формулу, по которой производится расчет. У калькуляторов имеется специальная клавиша, но лучше понять, как можно посчитать процент от числа самостоятельно. Ведь размер кредита, налоги, бонусы на работе – все исчисляется процентами. Любители шоппинга встречают их чаще, в периоды акций и распродаж.

Как происходит расчет, насколько он сложен? Стоит разобраться подробнее и с примерами.

Порядок вычисления

Начать стоит с элементарных понятий. Максимальное значение процентов – 100. Таким образом, процедура счета выглядит так:

1. Найти лишь 1% с числа. Для этого нужную величину необходимо поделить на максимальные 100%.
2. Затем, взяв полученный результат, умножить его на искомое число.

Расчет налогов

Например, НДС. Как известно, его величина – количество процентов, которые отнимаются с различных величин.

Процесс расчета:

• НДС – 20%;
• сумма товара – 300 рублей;
• размер налога – ?

Решение:

1. Найдите сначала 1%, поделив сумму товара на известные 100%

300/100% = 3 рубля (чтобы представить механизм счета, достаточно отнять два нуля от 300).

2. Определите, сколько в сумме составят 20%

300/3 * 20% = 60 рублей.

3. Получается, НДС для 300 рублей будет 60 рублей.
4. Итоговое значение вычисляется иначе:

300 * 0,2 = 60 рублей.

Это также правильный расчет, однако. Здесь проценты сначала переводятся в некий коэффициент, вот почему 20% стало 0,2. Затем сумму умножают.

Оба варианта – одинаково верные.

Обратный пример: как от суммы можно посчитать процент, какой алгоритм расчета применяется:

Задача неизменна – вновь необходимо отыскать 1% с указанного числа, разделяя его на максимальные 100%.  Затем результат вычисления поделить, взяв искомую цифру.

Процесс расчета:

• НДС – 60 рублей;
• сумма товара – 300 рублей;
• ставка налога – ?

Решение:

1. Первое действие аналогично вышеописанному примеру

300/100% = 3

2. Далее находим процент указанного НДС

60/3 = 20%

Метод пропорции

Многие считают его удобным и понятным, ведь формулы быстро забываются после школы. Пропорция же помогает расставить известные величины по приоритетным местам.

Сейчас для применения данной методики достаточно взять ручку, листок обычной бумаги и представить известные данные.

Пример расчета:

• зарплата – 10000 руб.;
• НДФЛ – 13%;
• «чистая» сумма для перевода – ?

Подобную задачу ежемесячно решают бухгалтера, кто начисляет сотрудникам зарплату. Ведь каждому нужно отнять значение НДФЛ и перечислить з/п «чистыми», без налога.

Решение:

1. В пропорции зарплата – известные 100%, а искомое число представлено Х

10000 – 100%

Х – 13%

Или

10000 / Х = 100% / 13%

2. Перевернув пропорцию, получим сумму НДФЛ:

Х = (13% х 10000) / 100%

3. Соответственно, ее необходимо отнять с общей начисленной зарплаты

10000 – 1300 = 8700 рублей – вот «чистый» оклад, который перечисляется безналом на карточку.

Расчет через Excel

Компьютеры помогают усовершенствовать методику расчета, особенно программа Excel. Главное ввести правильную формулу. Например, высчитать размер «чистого» оклада всем сотрудникам.

Бухгалтера любят Excel и порой заменяют ею калькуляторы.

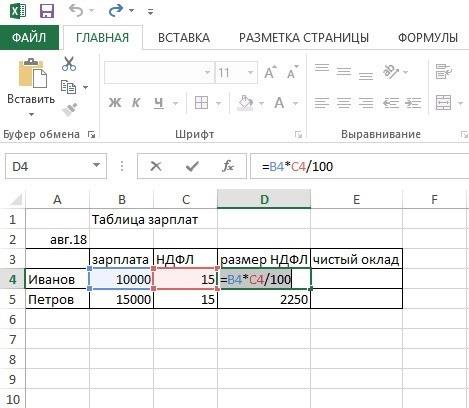
Вот пример обычной зарплатной таблицы, где слева перечислены фамилии, вторая колонка – зарплаты, третья – НДФЛ, а четвертая – размер налога. На ней вверху вводится формула. Ее видно, если навести туда курсор.

Формула: =B4*C4/100

Где вместо чисел – номера ячеек, где расположены нужные значения. Дополнительно указано деление (/100).

Достаточно ввести формулу на одну, верхнюю ячейку нужного столбца. Далее курсором зацепив уголок ячейки, провести ее вниз, тогда формула автоматически скопируется на остальные, нижние ячейки.

Видно, как система рассчитала значение «2250» НДФЛ.

Теперь осталось вычислить «чистый» оклад, для чего используется другая формула.

Экономические вычисления

Узнать фактический удельный вес различных чисел, ориентируясь на одно, итоговое значение. Подобное используется в статистике или экономике. Формула аналогичная, единственная разница – знаменатель всегда одинаковый. Для Excel это обозначается «$».

Формула:

A2/$B$2

Пример расчета:

Известно, сколько молока надоено всего и по сколько дала каждая корова. Нужно выяснить фактический удельный вес (размер вклада) каждой коровы.

Если известны лишь индивидуальные результаты, без одного, конечного значения, вычислить его поможет несложная формула: =СУММ(номер ячейки первый-последний). Аналогичным образом несложно проверить произведенный расчет значений удельного веса.

Видна формула, прописанная наверху.

Рассчитывается удельный вес.

Получается, все величины надоев автоматически делятся на одну, «86» конечную величину.

В конце столбика «удельный вес» после сложения вышло 100%, значит, расчет верен.

Темпы роста или же прироста показателя рассчитываются иначе:

1. Темп роста = прошедший период/текущий (в ячейке, где прописывается данная формула, устанавливается % формат).
2. Темп прироста = (текущий период – предыдущий)/предыдущий

Кредитная ставка: методы расчета

Каким образом банки подсчитывают ставки кредита?

Многие полагают, что расчет элементарный. Если кредит взят 10000 рублей, а период возврата – 1 год при ставке 10%, тогда считают:

10000/0,1 = 1000

Где 1000 будет платой, производимой клиентом банка за использование годового займа. Достаточно поделить ее на указанные 12 месяцев, чтобы выявить размер переплаты.

На деле банки используют другие методы. Учитываются факторы:

• начисление ставки – ежедневная, помесячная, годовая;
• продолжительность кредита;
• метод начисления.

Дифференцированная система

Считается выгодной, причем для заемщиков. Здесь можно сэкономить, уменьшая себе размер переплаты. Почему? Сначала перечисленные заемщиком средства погашают «тело» кредита, затем проценты. Сама ставка будет использована на остаток.

Используется формула сначала простых, потом сложных %. Смотря какая периодичность есть в их начислении.

Простые расчеты редки, они невыгодны банку.

Суть одна – переплата начисляется позднее, один раз, по окончанию.

Формула:

Fv = Sv * (1 + R * (Td/Ty))

Расшифровка значений:

• Fv – конечная сумма, оплачиваемая заемщиком;
• SV – размер займа, изначально выданного банком;
• R – ставка, указываемая в тексте договора;
• Td – срок, исчисляется месяцами, днями, годами или кварталами;
• Ty – количество периодов, используемых при совершении расчета (365 дней, возможно 12 месяцев, вместо них 4 квартала, 1 год).

Данная формула считается универсальной, может использоваться одинаково для кредита или для вычисления депозита.

Пример расчета:

• сумма кредита – 1000 рублей;
• срок – 10 месяцев;
• ставка – 10% (годовые);
• начисление – ежемесячное.

Решение:

1. Надо вернуть = 1000 (кредит) * (1+0,1*(10/12)) = 1083 рублей
2. Получается, переплата будет 81 руб.

Сложные проценты

Используется редко. Сложная методика, здесь при расчете кроме известных величин добавляется учет капитализации. Таким образом, к указанной первоначальной сумме добавляют начисленный доход, позднее, к полученной финальной сумме начисляют прибыль.

Особое внимание специалисты уделяют капитализации. Ее рассчитывают периодически, и частота использования указывается в тексте кредитного или же депозитного договора.

Например, проценты на созданный ранее депозит клиенту выплачивают ежегодно. Если он оставляет средства, не забирая, то сумма автоматически добавляется к имеющемуся депозиту. Второй год общую прибыль начисляют на другую итоговую сумму.

Формула:

Fv = Sv * (1 + (R/Ny))Nd

Расшифровка значений:

Fv – выявленная капитализированная величина;

Sv – значение первоначального депозита/займа;

R – указанная годовая ставка;

Ny – периоды капитализации (когда ее начисляют, временной период – год);

Nd – капитализированные периоды – общее количество.

Пример расчета:

• депозит клиента – 10000 рублей;
• ставка – 12 % (годовая);
• капитализация – ежемесячно;
• срок действия – год.

Решение:

1. Следуя формуле, подставляйте числа

10000 * (1+0,12/12)*12 = 11268

2. Таким образом, спустя год клиент вместо изначально вложенной им суммы получает 11268 рублей, где чистая прибыль – 1268 рублей

11268 – 10000 = 1268

3. Причем, клиентам наоборот, выгоднее сложные проценты, благодаря которой увеличивается используемая база расчета. Для кредита – простая методика. Однако, выбирает порядок расчета все равно банк.

Аннуитетная система

Тут большой разницы в выборе удобного расчета нет. Одинаково часто используется сложная или же простая формулы.

Суть одна – сумма имеющихся процентов, также величина долга будут распределены согласно продолжительности займа поровну. И клиент осуществляет ежемесячное погашение.

На страницах сайтов банков и просто онлайн имеются кредитные калькуляторы, через которые несложно самостоятельно рассчитать кредит, введя интересующие данные – сумму кредита, продолжительность займа.

В жизни расчет процентов оказывается полезным знанием, хоть люди стараются «на глаз» выявить его. Формулы удобнее, заодно они помогают узнать конкретное число, без гадания. Налоги, размеры депозита, кредитные ставки, распродажи – все это показано в процентах. Поэтому знать, как они вычисляются, безусловно полезно.