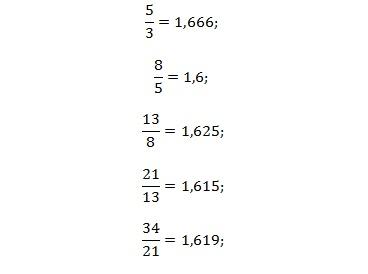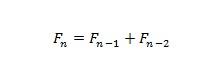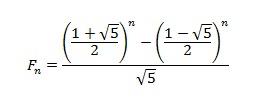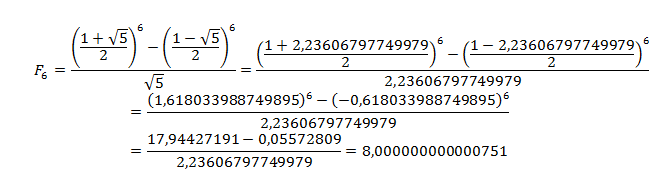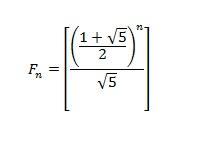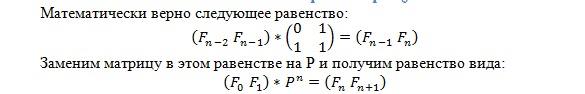Что такое числа Фибоначчи: формула

Числа Фибоначчи – это известная математическая последовательность чисел, которая нашла широкое применение в жизни человека, а также часто встречается в природе. Отсюда же пошло понятие «золотого сечения» — бытует мнение, что произведения архитектуры, построенные с учётом этого коэффициента, кажутся наиболее гармоничными и приятными глазу. Рассмотрим, как были открыты числа Фибоначчи, и какое применение они находят в повседневной жизни современного человека.

Сущность чисел Фибоначчи

В источниках можно встретить небольшое разночтение относительно того, с какого числа начинается последовательность Фибоначчи. Где-то она начинается с нуля:

0, 1, 1, 2, 3, 5, 8, 13…

А где-то она начинается с единицы:

1, 1, 2, 3, 5, 8, 13…

И тот, и другой вариант являются корректными. Главное, чтобы сумма 1 и 2 числа давала 3 число, сумма 2 и 3 числа давала 4 число, сумма 3 и 4 числа давала 5 число и так далее. А разночтения относительно нуля можно объяснить исходным примером, которым сам Леонардо Фибоначчи, математик эпохи позднего Средневековья, описывал свою последовательность. В его примере человек изолировал за стеной двух кроликов. Последовательность Фибоначчи отражает то, как будут размножаться эти кролики при условии, что каждый месяц, начиная со второго, каждая пара кроликов будет производить на свет одну пару кроликов.

Разумеется, это чисто теоретическая задача, которая не может воплотиться в реальной жизни. Однако числа Фибоначчи все-таки встречаются в природе – число лепестков у многих цветов всегда является числом Фибоначчи (например, у лилии). Число стеблей и цветков тысячелистника также всегда будет числом Фибоначчи. То есть процесс роста растения выглядит так. Был один стебель, который разделился на два. Какое-то время эти два ответвления растут поодиночке, затем один разделяется на два, их становится в общей сложности три. После следующего разделения их становится пять, и процесс повторяется снова и снова.

Золотое сечение

Если взять два любых числа из последовательности Фибоначчи и поделить большее на меньшее, то получится число, близкое к 1,618. Например:

Этот коэффициент пропорциональности носит название «золотое сечение». В эпоху Возрождения он широко использовался в архитектуре – сооружения, в которых соблюдены данные пропорции, считались более приятными глазу, гармоничными.

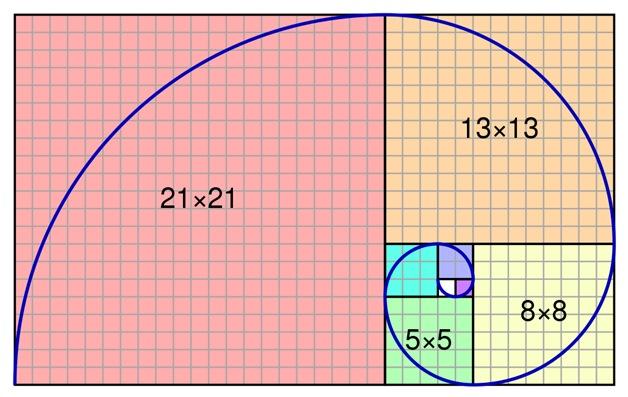
Наглядно эту пропорцию можно отобразить следующим образом. Пусть есть некая линия. Ее нужно поделить на два отрезка таким образом, чтобы соотношение меньшего отрезка к большему равнялось соотношению большего отрезка ко всей линии. Данный принцип отображается и в знаменитой спирали, построенной с учётом золотого сечения.

Примечательно, что и в природе встречаются такие спирали. Например, если присмотреться к расположению семян подсолнечника в соцветии, то можно разглядеть 2 спирали, одна из которых будет идти по часовой стрелке, другая – против. Если подсчитать количество семечек в каждой спирали, то это тоже будут числа Фибоначчи, причём соседние – например, 34 и 55.

Формула последовательности Фибоначчи

Математически эту последовательность можно представить в виде формулы:

Данная формула хорошо отображает закономерность, но никак не помогает с нахождением n-ного числа Фибоначчи. Поэтому существует другая формула, авторство которой приписывают математику Бине (впрочем, считается, что ещё до него она была известна Муавру).

Сложность заключается в том, что при расчётах нужно соблюдать высокую точность в вычислениях дробей. Для наглядности проведём расчёт 6 числа Фибоначчи.

Таким образом, мы получаем, что шестое число Фибоначчи равно 8. Но необходимость учитывать такое большое количество знаков после запятой существенно усложняет расчёты. Если округлять, то и точность результата будет не такой близкой.

Можно немного упростить расчёт. Вторая дробь всегда меньше единицы, поскольку квадратный корень из 5 всегда больше 1. Кроме того, значение этой дроби быстро стремится к нулю. Поэтому можно условно отбросить вторую дробь и сосредоточиться на расчёте только первой. Формула приобретает вид:

Квадратные скобки в данном случае указывают на то, что значение округляется до ближайшего целого. Тем не менее, посчитать так, скажем, 125 число Фибоначчи будет сложно, потому что нужна высокая точность в вычислениях.

Расчёт n-го числа Фибоначчи через матрицу

Смысл во всем этом таков, что достаточно возвести матрицу P в n-ную степень — и получится n-ное число Фибоначчи. Чтобы не утруждаться ручными расчётами, достаточно вычислить . Таким образом, нет необходимости считать дроби – расчёт числа Фибоначчи ограничится арифметикой целых чисел.

Практическое применение

Как уже упоминалось ранее, золотое сечение используется в архитектуре, а увлечённые биологи то и дело находят его в строении раковин, расположении листьев растений и др. Однако это принесёт мало практической пользы обычному человеку.

Числа Фибоначчи нашли практическое применение в анализе фондового рынка. Например, золотое сечение используется для предсказания, когда развернётся тренд. Считается, что цена начнёт развиваться в противоположную сторону примерно тогда, когда достигнет уровня 61,8% от предыдущего изменения.

Следовательно, участникам фондового рынка рекомендуется закрывать позиции незадолго до этого.

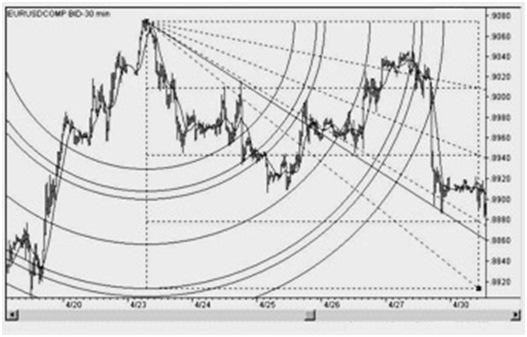
Кроме того, можно строить дуги. Для этого необходимо выбрать два экстремума – то есть наивысшие и наименьшие точки колебаний. Из вершины первого экстремума проводится горизонтальная линия, а из вершины второго – вертикальная линия. Далее выбираются коэффициенты — 0.333, 0.382, 0.4, 0.5, 0.6, 0.618, 0.666. Исследуемый отрезок делится на части, соответствующие этим коэффициентам – всем или нескольким. Если взять отношения 2/3 или 1/3, линии получатся более скоростными, а если придерживаться соотношений 0.618, 0.382, 0.5, то линии будут веерными.

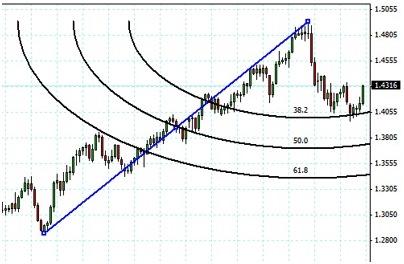
Затем рисуются лучи, выходящие из изначальной точки через выбранные точки. Должно получиться примерно такое:

В тех местах, где веерные дуги пересекаются с прямыми линиями, есть основания ожидать поворота тренда. Правда такой подход можно применять только для хороших импульсных движений. Проводить расчёты для каждого незначительного колебания не получится, да и не имеет смысла.

Подводя итог вышесказанному, можно отметить, что числа Фибоначчи – это не только любопытная математическая последовательность, встречающаяся даже в природе, но и закономерность, имеющая практическое применение. В частности, даже в теории циклов можно отметить схожесть их длин с числами Фибоначчи. Длина цикла (волны) по Кондратьеву равна 54 годам, что очень близко к 55 – числу Фибоначчи.