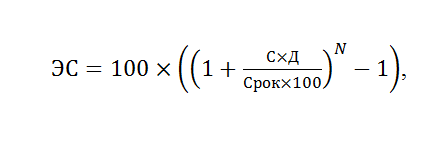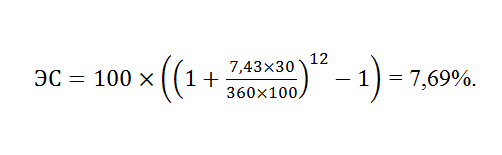нет комментариев
нет комментариев
Как правильно рассчитать проценты по вкладу
Несмотря на то, что ЦБ РФ в последние годы усилил надзор за деятельностью банков, многие кредитные учреждения по-прежнему предлагают розничным клиентам непрозрачные условия и делают акцент на «мелкий шрифт» в договоре. По этой причине каждый человек должен иметь представление о том, как рассчитать проценты по вкладу самостоятельно.
Для начала разберемся с финансовой терминологией. Вклад – это денежная сумма, которую физическое лицо предоставляет банку взаймы и получает за это регулярные проценты. Любой срочный депозит необходимо рассматривать именно с этой точки зрения, т.е. это не просто размещение лишних средств хоть под какую-нибудь ставку, а именно инвестиционная операция.
Процентная ставка – это «цена», под которую банк привлекает средства от своих вкладчиков на определённый договором срок. Процентный доход – это вознаграждение вкладчика, измеренное в денежном выражении. Часто его называют просто «проценты». Срок вклада – это период, на который заключается договор.Процентный период – это интервал, через который производится частичная или полная выплата набежавших процентов.
Простые проценты
Легче всего рассчитать доход по депозиту тогда, когда условиями договора предусмотрено начисление простых процентов без капитализации. При такой модели сумма вознаграждения зависит только от годовой ставки, срока договора и начальной величины вклада:
П = Срок*В*(С/100),
где:
П – проценты;
Срок – период размещения депозита.
В – сам вклад в денежном выражении;
С – ставка, %.
Рассчитаем доход:
П = 1*200*(8/100) = 16 тыс. руб.
В частном случае простые проценты могут перечисляться на расчётный счёт клиента по частям ежемесячно, ежеквартально или за полугодие. При такой схеме они рассчитываются пропорционально годовой ставке.
| Месяц | Проценты за месяц, руб. | Проценты нарастающим итогом, руб. |
|---|---|---|
| 1 | П = (1/12)*200000*8/100 = 1333 | 1333 |
| 2 | 1333 | 2666 |
| 3 | 1333 | 4000 |
| … | … | …. |
| 11 | 1333 | 14667 |
| 12 | 1333 | 16000 |
Сложные проценты
Прежде чем разбираться с формулой сложных процентов, вспомним, что такое капитализация вклада. Так называется опция, при действии которой процентные вознаграждения перечисляются не на отдельный расчётный счёт вкладчика, откуда он их может снимать на любые текущие нужды, а прибавляются к телу депозита.Соответственно, поскольку вклад увеличивается на сумму набежавших процентов, то и выплаты в последующих периодах также растут из-за приращения исходной базы. По этой причине необходимо чётко различать номинальную годовую ставку по вкладу и эффективную ставку.
— Регулярная проверка качества ссылок по более чем 100 показателям и ежедневный пересчет показателей качества проекта.
— Все известные форматы ссылок: арендные ссылки, вечные ссылки, публикации (упоминания, мнения, отзывы, статьи, пресс-релизы).
— SeoHammer покажет, где рост или падение, а также запросы, на которые нужно обратить внимание.
SeoHammer еще предоставляет технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Зарегистрироваться и Начать продвижение
Номинальная ставка прямо отражается в условиях договора. Например, если банк пишет, что привлекает вклады под 8% годовых, это она и есть. Тут всё просто.
Эффективная ставка (ЭС) – это фактическая ставка, рассчитанная по формуле сложных процентов, которая делает поправку на капитализацию. Как правило, банки её не описывают подробно в условиях договора, хотя встречаются случаи, когда кредитная организация предоставляет клиенту все расчёты до мельчайших деталей. Рассмотрим её формулу:
где:
- С – номинальная ставка;
- Д – продолжительность процентного периода в сутках, после завершения которого происходит капитализация;
- Срок – срок действия договора в днях;
- N – количество процентных периодов.
Формула выглядит угрожающе, поэтому сразу посмотрим реальную ситуацию.
Условия примера №3:
- ВТБ предложил физлицу в 2019 году открыть вклад «Время роста»;
- минимальный порог – 30000 руб.;
- номинальная ставка – 7,43% годовых;
- действует опция ежемесячной капитализации;
- срок вклада – 12 мес.
Необходимо:
- сначала рассчитать ЭС;
- затем подсчитать сумму годовых и ежемесячных процентов.
Поскольку условиями договора предусмотрена ежемесячная капитализация, это значит, что процентный период составляет 1 месяц, а параметр N будет равен 12. Для упрощения (округления) расчётов возьмём на вооружение германскую практику, по правилам которой один финансовый год принимается за 360 дней, а месяц за 30 суток:
Всё правильно, на своём официальном сайте банк ВТБ приводит аналогичную справочную ставку по этому капитализируемому вкладу. Расхождение в размере 0,01% можно списать на округления.
Теперь рассмотрим, как посчитать процентный доход, т.е. конкретную прибыль. Здесь есть два подхода, первый – можно просто умножить величину первоначального вклада на эффективную ставку. В результате мы получим сумму причитающихся процентов за весь год:
П = 30000*(7,69/100) = 2307 руб.
Этот метод является классическим, да и если смотреть на вещи объективно, то ради такого упрощения и используется ЭС. С другой стороны, если банк позволяет в любое время расторгнуть договор с полным сохранением набежавших процентов за прошедшие периоды, есть смысл рассчитывать суммы отдельно для каждого месяца.
Проще всего это сделать по формуле простых процентов для каждого месяца в отдельности, последовательно прибавляя к сумме вклада начисленные вознаграждения за «закрытые» периоды.
| Месяц | Величина депозита на начало месяца | Формула для расчёта суммы процентов | Сумма процентов, руб. |
|---|---|---|---|
| 1 | 30000 | (1/12)*30000*7,43/100 | 185,75 |
| 2 | 30185,75 | (1/12)* 30185,75*7,43/100 | 186,90 |
| 3 | 30372,65 | (1/12)* 30372,65*7,43/100 | 188,06 |
| 4 | 30560,71 | ||
| …. | и т.д. |
Ещё есть вариант с дисконтированием, но он не менее трудоёмок, поэтому мы его рассматривать не станем.
Как на доходность вклада влияет пролонгация
Пролонгация – это продление срочного депозита после завершения предыдущего договора, если клиент не подал распоряжение на вывод средств. Как правило, в этом случае основные условия вклада остаются прежними, а корректируется лишь ставка, что логично, ведь макроэкономические показатели постепенно меняются.
— Разгрузит мастера, специалиста или компанию;
— Позволит гибко управлять расписанием и загрузкой;
— Разошлет оповещения о новых услугах или акциях;
— Позволит принять оплату на карту/кошелек/счет;
— Позволит записываться на групповые и персональные посещения;
— Поможет получить от клиента отзывы о визите к вам;
— Включает в себя сервис чаевых.
Для новых пользователей первый месяц бесплатно. Зарегистрироваться в сервисе
В момент автоматического продления вклада величина нового депозита определяется с учётом набежавших процентов по старому договору, поэтому при расчёте итоговой прибыли после нескольких пролонгаций необходимо руководствоваться скорректированной формулой сложных процентов.
Эффективная ставка для всего периода (с учётом всех пролонгаций) будет иметь следующий вид:
ЭС = 100*((1+С1*/100)*(1+С2*/100)*…..*(1+Сn*/100) -1)), где:
- C1 –ставка в первый год;
- С2 – ставка во второй год;
- Сn – ставка в последний год.
Сначала рассчитаем эффективную ставку для всего трёхлетнего периода:
ЭС = 100*((1+5*/100)*(1+6*/100)*(1+5,5*/100) -1)) = 17,4215%
Далее умножаем первоначальную сумму вклада на ЭС:
П = 100000 *17,4215/100 = 17421,5 руб.
Если условиями вклада предусмотрена ежемесячная или квартальная капитализация, то номинальные ставки в формуле потребуется заменить на годовые ЭС. Проще говоря, появится ещё одно арифметическое действие.
В теории с пролонгацией всё просто, но на практике подобные расчёты могут пригодиться только для контроля за действиями банка (уже по факту произведённых начислений и выплат), ведь клиент заранее на знает, как в момент продления договора через N лет изменится номинальная ставка.
Вклады с меняющейся ставкой
Достаточно часто банки практикуют маркетинговые уловки, которые условно можно назвать «обещаем ставку до». В чём их суть: клиенту предлагается вклад под высокую ставку, значительно превышающую рыночную, но на деле оказывается, что этот «вкусный» процент начисляется лишь за пару месяцев, а всё остальное время по вкладу выплачиваются небольшие вознаграждения.
| I квартал | II квартал | III квартал | IV квартал | |
|---|---|---|---|---|
| Ставка | 4% | 5% | 7% | 9% |
В таблице выше представлен пример предложения в стиле «получайте до 9% годовых». Как видим, здесь высокие проценты выплачиваются лишь в четвёртом квартале, но из-за низких ставок в первом полугодии реальная доходность такого вклада не будет сильно выделяться среди предложений конкурентов.
Рассмотрим, как посчитать годовые проценты в этом случае.
Для всех вычислений будет достаточно формулы простых процентов, единственное, что здесь необходимо учесть, так это пропорции, ведь ставки установлены не на год, а отдельно для каждого квартала.
| Квартал | Проценты за месяц, формула | Проценты, руб. |
|---|---|---|
| 1 | П = (3/12)*100000*4/100 | 1000 |
| 2 | П = (3/12)*100000*5/100 | 1250 |
| 3 | П = (3/12)*100000*7/100 | 1750 |
| 4 | П = (3/12)*100000*9/100 | 2250 |
| Итого | 6250 |
Осталось определить эффективную ставку:
ЭС = 100*(6250/100000) = 6,25%
Получается, что реально вкладчик получает всего 6,25% годовых. С другой стороны, всё правильно – это значение укладывается в заявленный банком интервал «до 9%», поэтому никаких нарушений с его стороны нет.
Так как формула сложного процента здесь получается весьма значительная и трудночитаемая, будет разумно вынести алгоритм расчётов в подробную таблицу.
| Месяц | Величина депозита на начало месяца | Формула для расчёта суммы процентов | Сумма процентов, руб. | Величина депозита на конец месяца |
|---|---|---|---|---|
| 1 | 100000 | (1/12)*100000*4/100 | 333 | 100333 |
| 2 | 100333 | (1/12)*100333*4/100 | 334 | 100668 |
| 3 | 100668 | (1/12)*100668*4/100 | 336 | 101003 |
| 4 | 101003 | (1/12)*101003*5/100 | 421 | 101424 |
| 5 | 101424 | (1/12)*101424*5/100 | 423 | 101847 |
| 6 | 101847 | (1/12)*101847*5/100 | 424 | 102271 |
| 7 | 102271 | (1/12)*102271*7/100 | 597 | 102868 |
| 8 | 102868 | (1/12)*102868*7/100 | 600 | 103468 |
| 9 | 103468 | (1/12)*103468*7/100 | 604 | 104071 |
| 10 | 104071 | (1/12)*104071*9/100 | 781 | 104852 |
| 11 | 104852 | (1/12)*104852*9/100 | 786 | 105638 |
| 12 | 105638 | (1/12)*105638*9/100 | 792 | 106431 |
Итого за год при ежемесячной капитализации будет получено 6431 руб. Эффективная ставка составляет 6,43%.
Расчет реальных ставок
Рассматривая вопрос о том, как рассчитать проценты по вкладу, хотим напомнить об инфляции, ведь она постепенно «съедает» сбережения. Чтобы узнать фактическую эффективность банковского вклада, необходимо освоить и расчёт реальной ставки.
Многие люди с этой целью просто вычитают из ставки по вкладу инфляцию, но это некорректный подход, правильнее будет использовать более сложный метод. Он состоит из нескольких этапов:
- Сначала рассчитывается соотношение R = (1+ЭС/100)/(1+И/100), где ЭС и И – это эффективная ставка и инфляция в %.
- Далее первоначальная величина депозита умножается на R. В результате получается сумма на конец действия вклада, номинированная в текущих ценах.
- Затем оценивается прирост этого реального депозитав процентах.
Следовательно, коэффициент R будет равен:
R = (1+0,0643)/(1+0,045) = 1,0185
Теперь умножаем первоначальный вклад на R:
В = 100000*1,0185 = 101850 руб.
В переводе на понятный язык это значит, что реальное благосостояние вкладчика банка за 2019 год увеличится в 1,0185 раз.
И на последнем этапе определяем реальную ставку по вкладу:
РС = 100*(101850-100000)/100000 = 1,85%
А теперь предположим, что на самом деле инфляция составляет не 4,5%, а 8%. В этом случае порядок расчёта реальной ставки по депозиту будет следующий:
- R = (1+0,0643)/(1+0,08) = 0,985;
- В = 100000*0,0985 = 98500 руб.;
- РС = 100*(98500-100000)/100000 = -1,5%.
Вывод – фактическая покупательная способность вкладчика под влиянием инфляции снизилась на 1,5%. Даже размещение денег в банке под 6,43% годовых не помогло защитить средства от обесценивания.