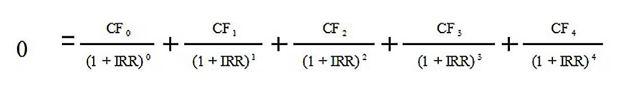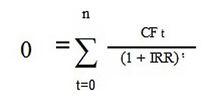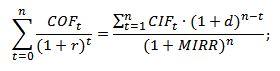Внутренняя норма доходности — Формула IRR

Внутренняя норма доходности – это показатель, помогающий оценить доходность инвестиций. Он показывает, при какой доходности прибыль инвестора будет равняться его затратам. Метод IRR хорошо применять, когда нужно сравнить два проекта, или же соотнести стоимость инвестиционных ресурсов с последующей прибылью от их вложений.

Как это работает

Выбирая варианты вложения свободных денег, инвестор всегда стремится выбрать наиболее доходный вариант. Иногда это просто – если банк А предлагает депозит под 4% годовых, а банк Б открывает вклады под 6,5% годовых, то очевидно, что предложение банка Б принесёт больший доход.

Однако далеко не по всем вариантам инвестиций доходность известна в такой форме, которую можно легко оценить и сравнить.

Например, гражданин Яблоков имеет в распоряжении 3 млн. рублей. Он может положить эти средства на депозит в банке, либо купить квартиру и получать доход в виде арендной платы. Соотнести рентабельность этих двух вариантов не так-то просто, и здесь приходит на помощь IRR.

Экономический смысл показателя сводится к двум тезисам.

• Чем выше IRR, тем выше доходность проекта. Следовательно, если инвестор колеблется между несколькими вариантами, рекомендуется выбирать тот проект, у которого выше IRR.
• IRR можно воспринимать как предельную стоимость инвестиционных ресурсов. Если инвестор использует для вложений заёмные средства, то ему имеет смысл брать кредит по ставке меньше IRR или равной ей, но ни в коем случае не больше. В противном случае инвестор понесёт убытки.

Формула IRR

Для расчёта IRR берётся формула чистого приведённого дохода, только сам NPV приравнивается к нулю. Таким образом, в результате находится то значение IRR, при котором прибыль от вложений равняется инвестиционным затратам.

CF в данном случае – денежный поток, приносимый вложением в каждом году. В сокращённом виде это выглядит так:

После подстановки величин денежных потоков получается уравнение, которое можно решить, зная базовые правила математики. Однако можно пойти более простым и быстрым путём – воспользоваться формулой в Excel.

Расчёт IRR через Excel

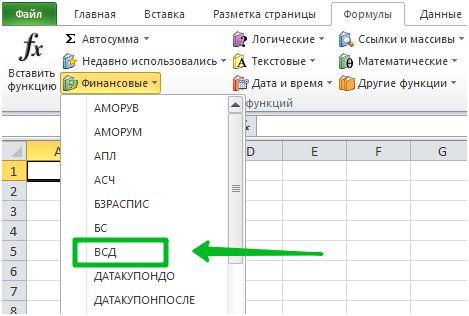
Данный показатель здесь называется не «внутренняя норма рентабельности», а «внутренняя ставка доходности», и обозначается аббревиатурой ВСД. Не стоит пугаться разницы в наименованиях, это один и тот же показатель.

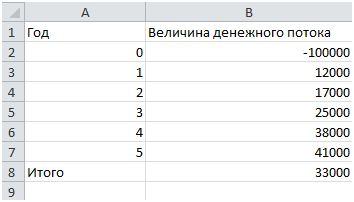
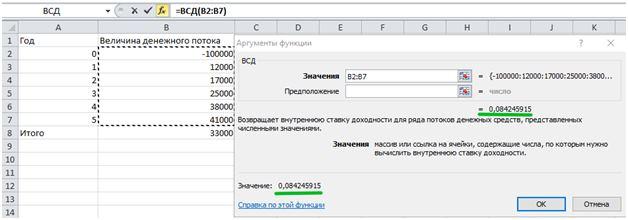
Для расчёта IRR по такому методу необходимо заполнить табличку следующего вида.

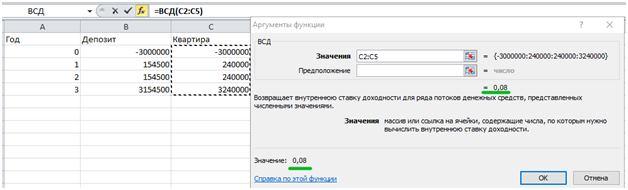
Затем нужно выбрать функцию ВСД на вкладке «Финансовые» и задать диапазон, где приведены значения величин денежного потока. Excel автоматически подсчитает значение IRR в том же окне.

То есть, в данном абстрактном примере IRR равняется ~8,42%. При ставке доходности 8,42% инвестор возместит вложенные 100 тыс. рублей, но прибыли не получит.

Возможные ошибки при расчёте IRR через Excel

Ошибка #ЧИСЛО! может показываться в двух случаях:

• Введённые данные не соответствуют исходным параметрам, из-за чего невозможно произвести математические вычисления.

Так, чтобы NPV мог равняться нулю, необходимо, чтобы была как минимум одна отрицательная величина (это исходные вложения инвестора) и одна положительная величина (приносимый доход).

Если будут только отрицательные величины, то проект заведомо убыточен, и ни о какой внутренней норме рентабельности не может идти и речи. Если же будут только положительные величины, то NPV также никак не сможет равняться нулю.

• Неудачная попытка вычислений.

Excel находит величину IRR путём подстановок возможных значений и совершает для этого 20 попыток. Если вбить в программу большое количество периодов (например, ежемесячные поступления на протяжении пяти-десяти лет), Excel может не справиться с задачей и не подобрать величину IRR за двадцать попыток. Тогда выдаётся ошибка #ЧИСЛО!

Чтобы избежать этого, можно ввести предполагаемое значение IRR в поле «предположение». Не страшно, если значение будет приблизительным – суть в том, чтобы помочь программе сузить диапазон подбора. В случае с простыми расчётами это поле можно оставлять пустым, программа сама справится.

Теперь вернёмся к примеру с гражданином Яблоковым и рассмотрим расчёт IRR на примере конкретных инвестиционных проектов, с которыми сталкивается обычный человек.

Пример расчёта IRR

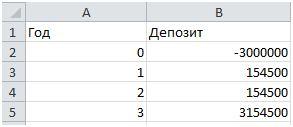
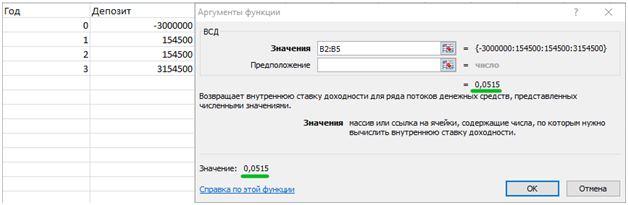
Допустим, Яблоков вложил свои 3 миллиона на депозит в Сбербанке. Срок вклада – 3 года, ставка 5,15% годовых. Вклад открывается без капитализации, проценты снимаются ежегодно, дабы наглядно видеть приток денег от инвестирования.

Как легко можно догадаться, IRR будет равняться ставке по депозиту. То есть, если эти деньги Яблоков сам накопил или получил в наследство, и не платит за пользование ими никаких процентов, то такой вариант вложений всегда будет доходным. А внутренняя норма доходности будет равняться ставке по вкладу.

Теперь рассмотрим вариант с покупкой квартиры и сдачей в аренду.

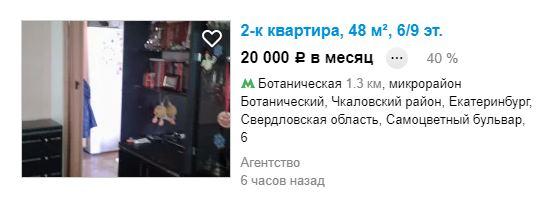
Предположим, наш Яблоков живёт в Екатеринбурге. Если обратиться к объявлениям на Авито, то за 3 миллиона можно приобрести двухкомнатную квартиру.

Для чистоты эксперимента было выбрано случайное объявление. Предположим, что оставшиеся 150 тысяч Яблоков потратил на косметический ремонт купленной квартиры или услуги риелтора и др.

Далее определяем размер потенциального дохода. Была выбрана сдаваемая в аренду двухкомнатная квартира такой же площади, на той же станции метро.

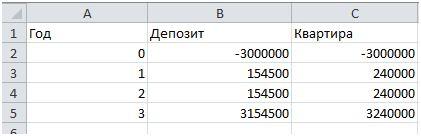
Предположим, Яблоков нашёл арендаторов на 3 года, которые будут платить 20 тыс. руб. в месяц. Таким образом, за год Яблоков будет получать 240 тыс.

Таблица для расчёта выглядит следующим образом.

Разница в доходах заметна визуально. Расчёт IRR подтверждает это.

Внутренняя норма рентабельности для депозита равняется 5,15%, т.е. его ставке, а для покупки квартиры в качестве инвестиционного проекта внутренняя норма доходности составит 8%. Из двух проектов инвестору рекомендуется выбирать тот, который принесёт большую доходность, т.е. проект с более высоким значением IRR.

Тем не менее, метод IRR не лишён недостатков и подходит не всегда. Одна из главных проблем – это множественность IRR.

Проблема множественности IRR

Чтобы понимать причины возникновения этой проблемы, необходимо разобраться с понятиями ординарного и неординарного денежного потока.

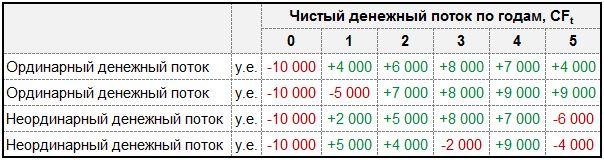
Для инвестиционного проекта нормально сначала требовать затрат, а потом понемногу начинать приносить прибыль. Поэтому, если поток один раз меняет знак с минуса на плюс, то он считается ординарным. Если же поток уже начал приносить прибыль, а потом внезапно потребовал вложений, то такой денежный поток будет считаться неординарным.

По таблице видно, что даже если проект два года подряд убыточен, это все равно считается ординарным потоком. Главное, чтобы до окончания срока вложение не уходило в убыток.

На нашем примере такое представить сложно. Допустим, в квартире разбили окно не по вине арендаторов, и Яблокову пришлось из своего кармана оплатить установку нового стеклопакета. Или же арендаторы съехали, квартира пустовала месяц, и Яблоков из своего кармана оплачивал коммунальные услуги, то послужило убытком.

В нашем примере речь идёт о примере инвестирования в недвижимость для физического лица, но в бизнесе такие проекты, которые уже на этапе эксплуатации и принесения доходов требуют вложений, далеко не редкость.

В таком случае при расчёте IRR выходит два действительных корня, что исключает возможность получения однозначного ответа. Инвестор может оценить подобное вложение по методу чистого приведённого дохода или воспользоваться формулой MIRR – модифицированной внутренней нормы доходности.

Модифицированная внутренняя норма доходности (MIRR)

По формуле MIRR можно оценить доходность инвестиций, когда проект требует вложений не только на начальном, но и на последующих этапах.

Изначально это уравнение состоит из двух частей.

где COF_t – отток денежных средств в периоде t (cash outflow);

CIF_t – приток денежных средств в периоде t (cash inflow);

r – ставка дисконтирования;

d – ставка реинвестирования денежных ресурсов;

n – количество периодов, т.е. срок действия проекта или инвестиционный горизонт.

Как и с IRR, для упрощения расчётов можно прибегнуть к функциям Excel. MIRR рассчитывается через функцию МВСД, которая также находится в разделе финансовых функций.

Для расчёта понадобится ввести размеры денежных потоков, ставку дисконтирования и реинвестирования.

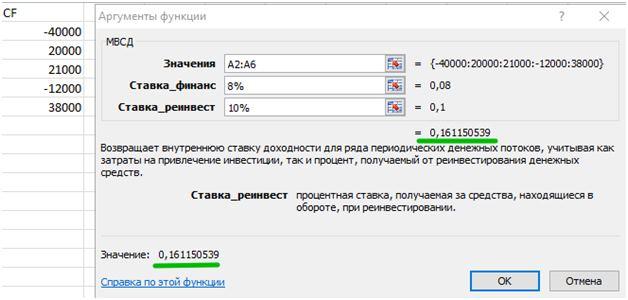
Расчёт MIRR для абстрактного проекта, по которому ожидается отток денежных средств, будет выглядеть следующим образом.

Показатель MIRR в 16,11% будет означать, что при внутренней норме доходности 16,11% инвестор компенсирует все свои вложения в проект, но не будет иметь прибыли.

Сравнение IRR и MIRR

MIRR позволяет рассчитывать внутреннюю норму доходности для проектов с неординарным денежным потоком. Однако это не единственное отличие данного показателя от IRR.

В MIRR учитывается ставка реинвестирования полученных денежных  потоков. В формуле IRR этот момент никак не отображается – подразумевается, что реинвестирование будет происходить по той же ставке IRR. На практике это не всегда реально.

С другой стороны, учёт ставки реинвестирования вызывает другую возможную неточность. Если MIRR рассчитывается для долгосрочного проекта, то маловероятно, что на протяжении всего этого срока ставка реинвестирования останется прежней. Несмотря на это, в целом MIRR даёт более точную оценку инвестиционного проекта.

Тем не менее, при расчёте IRR и MIRR инвесторы сталкиваются с проблемами прогнозирования денежных потоков. Даже опытным специалистам бывает сложно адекватно оценить размеры планируемых поступлений от проекта, из-за чего расчёты не всегда оказываются достоверными.

Вопреки недостаткам и возможным проблемам с расчётом IRR по-прежнему остаётся распространённым и часто используемым методом оценки рентабельности проекта. Она позволяет понять, стоит ли вкладываться в тот или иной проект, а также помогает выбрать наиболее выгодный проект из нескольких вариантов.