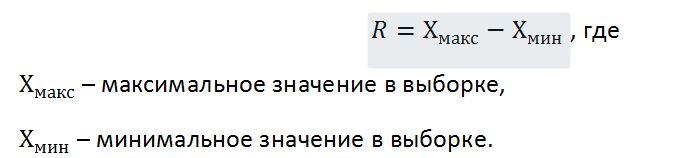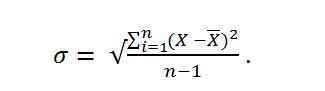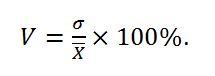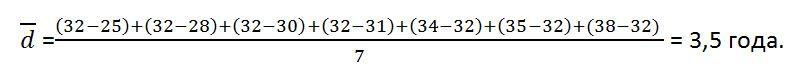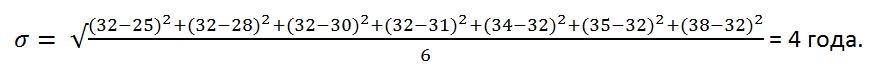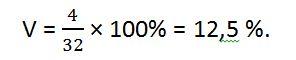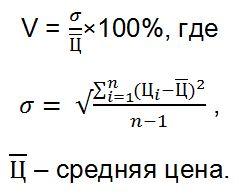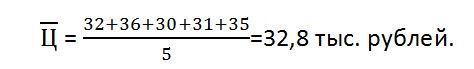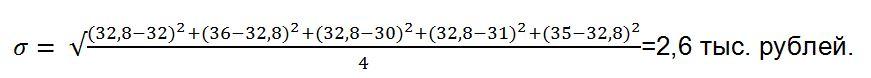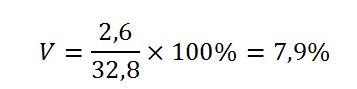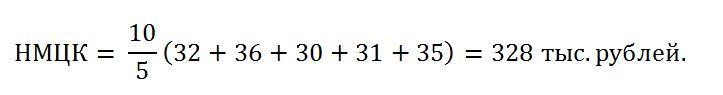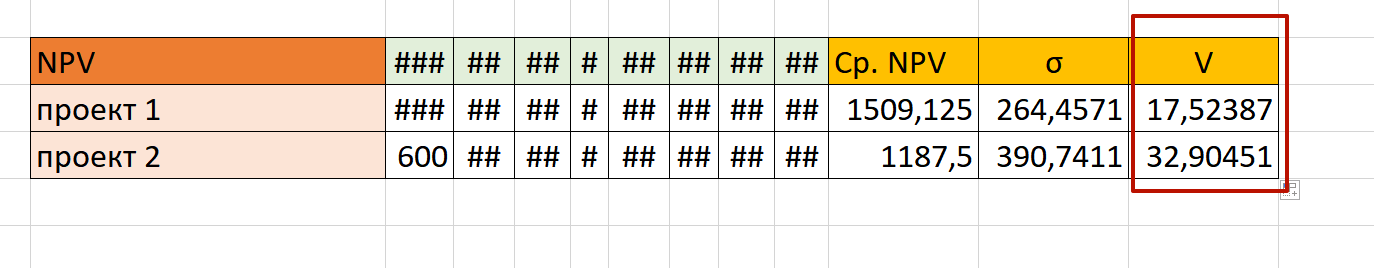Что такое коэффициент вариации и для чего он нужен

Коэффициент вариации – это статистический показатель, который широко используется в финансовых расчетах. Он показывает степень разброса значений в числовой последовательности. А именно, насколько каждая из величин отклоняется от средней. Если вариация слишком высока, то оценивать среднее значение некорректно. В этой ситуации обычно исключают минимальное и максимальное число.

Показатель чаще всего применяется при формировании начальной минимальной цены контракта по 44-ФЗ. Она должна основываться на выборке рыночных цен, а в их оценке как раз и используется вариация. Кроме того, применяется при анализе рисков инвестиционных проектов и доходности ценных бумаг. В целом, показатели вариации применимы в любой сфере, где требуется оценить совокупность данных и их разнообразие: статистика, математика, экономический анализ, социология, маркетинг и т.д.

Формулы расчета в статистике

Для оценки совокупности значений и их однородности применяют следующие инструменты:

1. Размах вариации – разница между минимальным и максимальным значением:
2. Среднее линейное отклонение – насколько в среднем значения в выборке отличаются от среднего:
3. Среднеквадратичное отклонение – квадратный корень из дисперсии, а именно из квадрата суммы отклонений каждой величины от средней, деленной на количество этих величин минус 1:
4. Коэффициент вариации – относительное отклонение каждого из значений от среднего:

Рассмотрим применение указанных формул на примере оценки среднего возраста работающих в отделе кадров. В указанном подразделении трудятся 7 сотрудников, которым 25, 28, 30, 31, 34, 35 и 38 лет. Размах вариации покажет нам разницу в возрасте между самым младшим и самым старшим из них:

R = 38 – 25 = 13 лет.

Рассчитаем среднее линейное отклонение. Для этого для начала найдем средний возраст в отделе: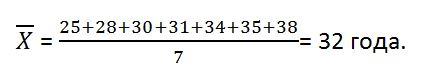Теперь посчитаем среднее линейное отклонение:

Соответственно, мы можем сказать, что средний возраст сотрудников составляет 32 ± 3,5 года.

Среднеквадратичное отклонение покажет то же самое, но более точно:

Коэффициент вариации покажет, на сколько процентов возраст каждого работника отличается от среднего по отделу:

Оценка коэффициента вариации

Если со средними значениями и отклонениями от них все понятно, то зачем же рассчитывается коэффициент вариации? С его помощью можно судить, насколько показательно усредненное значение и можно ли по нему судить о выборке в целом. В нашем примере он позволит ответить на вопрос, можно ли утверждать то, что средний возраст по отделу кадров составляет 32 года. Либо реальные показатели будут слишком сильно отличаться от полученного значения?

В статистике определены следующие критерии оценки:

• менее 10 % — разброс значений незначительный;
• 10% — 20% — вариативность средняя;
• 20% — 33% — значительная неоднородность;
• более 33% — выборка неоднородна.

Если показатель вариации превышает 33%, то выборка считается неоднородной и судить о ней по средним значениям никак нельзя. При незначительном разбросе достоверность средних будет максимальной. В нашем примере вариативность средняя и в целом оценивать возраст по средним значениям с учетом отклонений вполне можно.

Если посмотреть на числовой ряд, то видно, что только 2 сотрудника существенно отклоняются от среднего возраста. На практике при слишком высокой вариативности из анализа исключают максимальное и минимальное значения, после чего проводят повторную проверку. Также часто по коэффициенту вариации сравнивают разные выборки. В нашем примере это слабо применимо, но, например, при анализе цен конкурентов будет вполне эффективно для выбора наиболее подходящей для анализа совокупности значений.

Применение при закупках по 44-ФЗ

Федеральный закон 44-ФЗ регулирует порядок проведения государственных закупок. Его цель – не допустить злоупотреблений должностных лиц и передачу контрактов «своим» фирмам по завышенным/заниженным ценам. Именно для этого в законе определен порядок того, как устанавливается начальная минимальная цена контракта (НМЦК) – та, с которой и будут начинаться торги.

Методика определения начальной минимальной цены

Законом предусмотрено 5 методов определения НМЦК:

1. Метод сопоставимых рыночных цен (анализа рынка).
2. Тарифный.
3. Нормативный.
4. Проектно-сметный.
5. Затратный.

При этом наиболее предпочтительным и рекомендуемым является именно первый. Его суть в том, что анализируются цены точно таких же товаров или услуг (идентичных) либо при их отсутствии схожих (однородных). Оба понятия четко определены:

• идентичные товары или услуги – имеющие одинаковые характерные признаки (без учета различий внешнего вида);
• однородные – имеющие похожие характеристики и компоненты, взаимозаменяемы по назначению.

Данный порядок определен статьей 22 вышеуказанного закона. В 2019 году в нее было внесено несколько изменений:

• к работам, которые необходимо оценивать проектно-сметным методом, добавлен снос зданий;
• добавлен пп. 23, определяющий публикацию информации в единой информационной системе;
• если объем контракта определить невозможно, то заказчик определяет ценовые параметры закупки в соответствии с методиками, указанными в законе.

Как рассчитать НМЦК

Для расчета начальной цены заказчику необходимо составить выборку рыночных цен. Это можно сделать следующими способами:

• отправить поставщикам запросы на коммерческое предложение;
• найти в реестрах уже заключенных контрактов;
• воспользоваться общедоступными способами поиска информации – каталогами, базами данных и т.д.

Обычно используется первый способ. Нескольким поставщикам отправляются запросы установленной формы, а на основании полученных ответов и осуществляются расчеты по следующей формуле:

Коэффициент вариации в данном случае примет вид:

Пример расчета

Рассмотрим, как рассчитать НМЦК и коэффициент вариации на примере закупки 10 холодильников для больницы. От 5 поставщиков были получены коммерческие предложения со следующими ценами: 32, 36, 30, 31 и 35 тыс. рублей за штуку.

Оценим однородность ценовых предложений путем расчета коэффициента вариации. Для начала рассчитаем среднюю цену:

Теперь необходимо найти среднеквадратичное отклонение:

И, наконец, рассчитываем коэффициент вариации:

V меньше 10%, таким образом, делаем вывод о том, что выборка однородна и ее можно использовать для установки закупочных цен для торгов.

Посчитаем минимальную цену контракта:

Использование в оценке рисков

В финансовом анализе степень отклонения показателя от среднего значения показывает уровень риска. Например, если прибыль в разные годы существования компании то существенно поднимается, то падает в убыток, инвестировать в нее опасно. То же самое касается ценных бумаг и любых других биржевых инструментов. Самыми привлекательными будут стабильные бумаги с минимальными колебаниями котировок при хорошем росте. Таким образом, есть еще два направления, где активно используется коэффициент вариации: оценка рисков проекта и рисков по доходности ценных бумаг.

Инвестиционные проекты

Как правило, при оценке рисков инвестиционных проектов используются:

• ряд значений чистой приведенной стоимости (NPV) по годам;
• аналогичные показатели по IRR;
• разброс вероятности потери прибыли, рентабельности и т.д. в зависимости от изменения какого-либо условия (цены, объема продаж и т.д.).

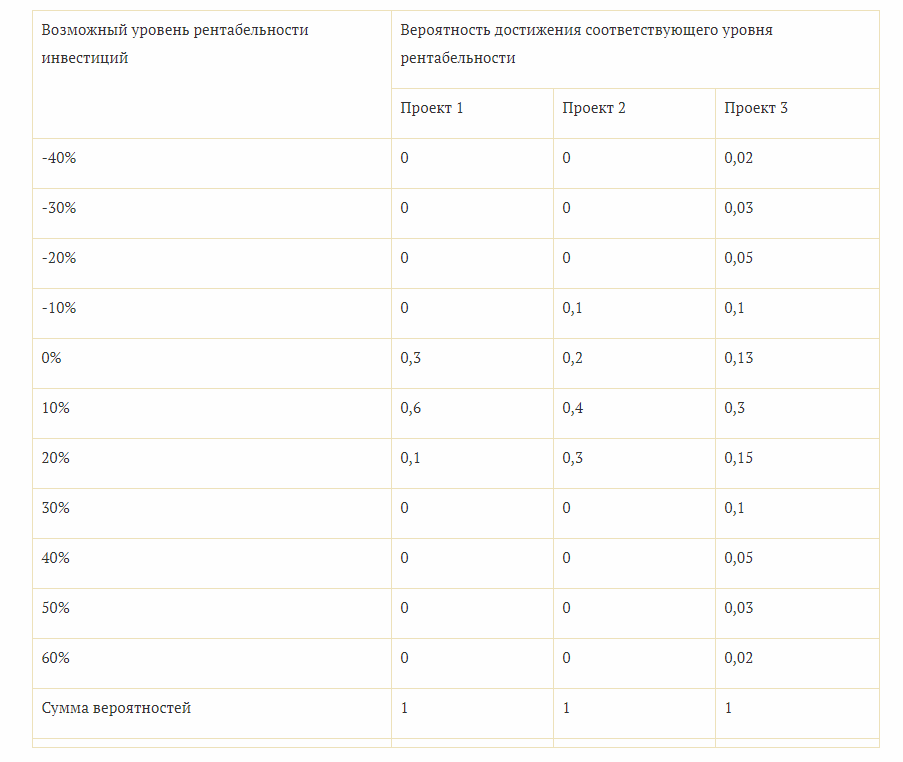
Обычно сравниваются несколько проектов по всем критериям. Также есть вариант рассмотреть возможность достижения того или иного уровня рентабельности:

В данном случае все проекты будут рискованными, поскольку коэффициент вариации составит 65%, 95% и 198% соответственно. Но риск по первому более чем в 2 раза ниже, чем по третьему, поэтому из представленных вариантов лучше выбрать его.

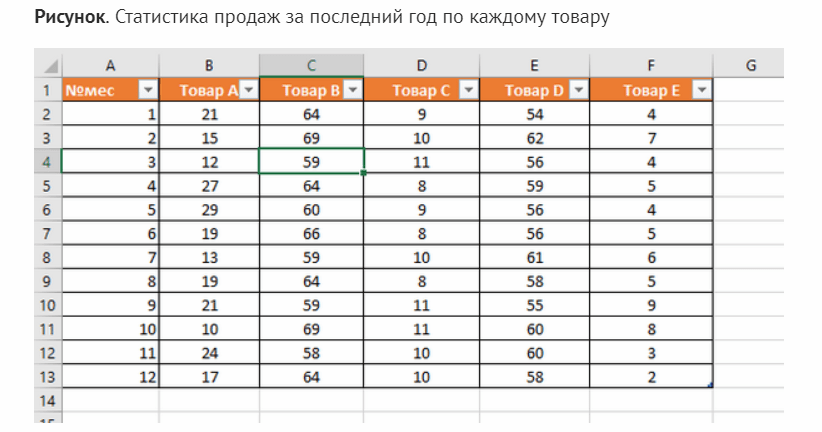
Нередко используют коэффициент при анализе спроса и принятии решении о закупках. Например, анализируется статистика продаж товара, после чего определяется, что закупать в первую очередь, а что только при наличии предзаказа:

В данном примере коэффициенты вариации по товарам А, B, C, D и E будут равны 30%, 6%, 12%, 4%, 38% соответственно. Очевидно, что спрос на продукцию E нестабилен и сильно колеблется в разные месяцы, поэтому заказывать целую партию рискованно.

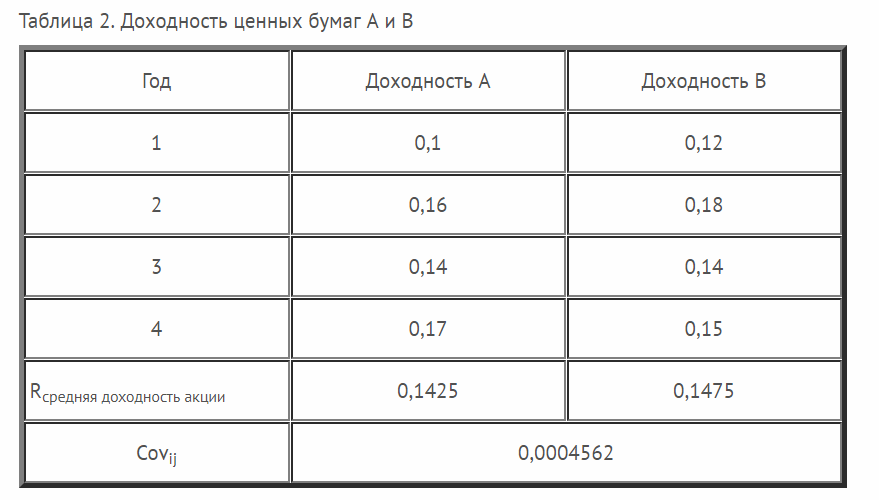
Ценные бумаги

Что касается торговли на бирже, то здесь можно оценивать в двух вариантах:

• доходность инструмента за временной период;
• доходность ценных бумаг в составе портфеля.

В первом случае, имея данные о колебаниях котировок в прошлом, мы сможем оценить риск вложения именно в данный инструмент. Во втором варианте можно оценить риск портфеля инвестиций на основании совокупности доходности каждой его составляющей. Также риск портфеля можно проанализировать на основании совокупности вариаций каждой его составляющей во временном промежутке. Все эти методики используются в комплексном анализе рисков инвестиционного портфеля.

Расчет в MS Excel

Как при расчете цены контракта, так и при оценке инвестиционных проектов выполнять громоздкие вычисления квадратичного отклонения и коэффициента вариации вручную очень трудоемко. Поэтому рассмотрим, как быстро и просто выполнить это при помощи электронной таблицы Excel.

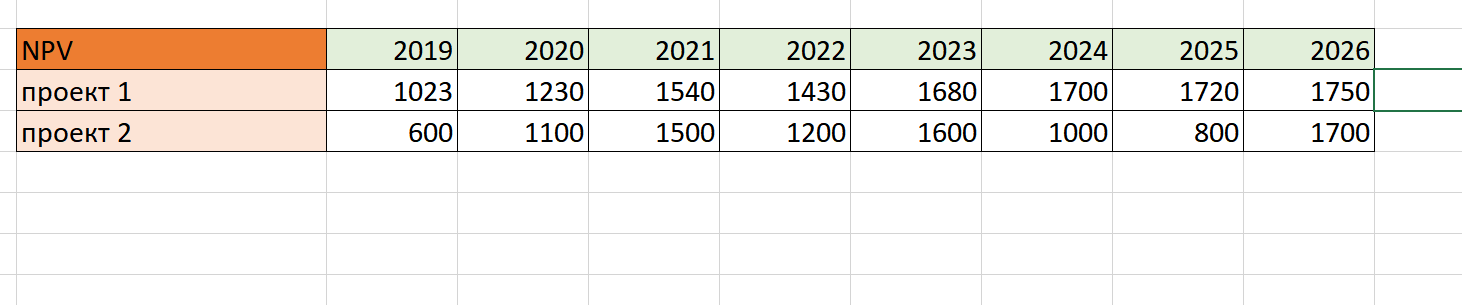
Для начала открываем редактор и создаем таблицу с исходными данными. Для примера возьмем два инвестиционных проекта с показателями NPV за 8 лет.

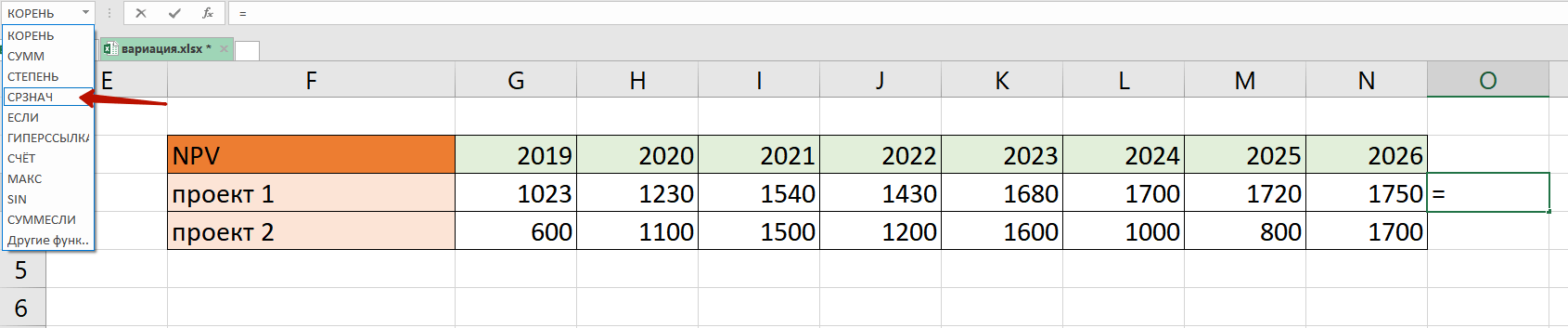
Далее находим среднее значение прибыли при помощи функции СРЗНАЧ:

Получились вот такие значения:

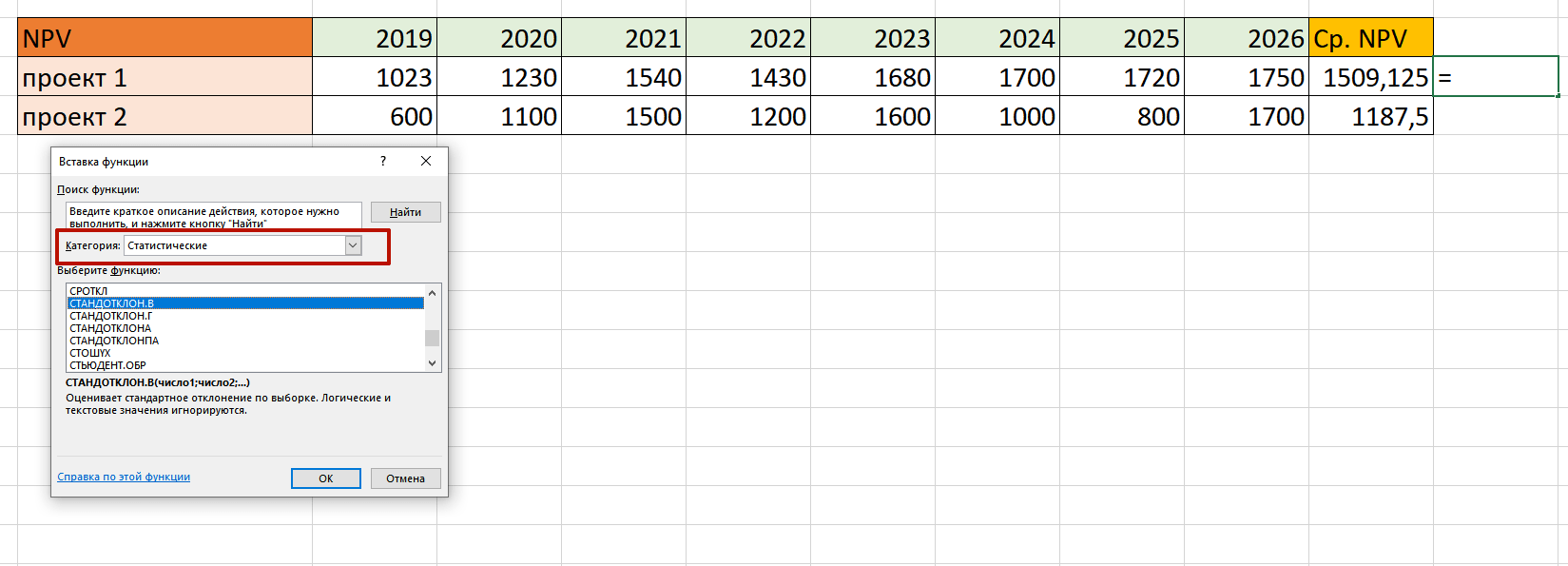
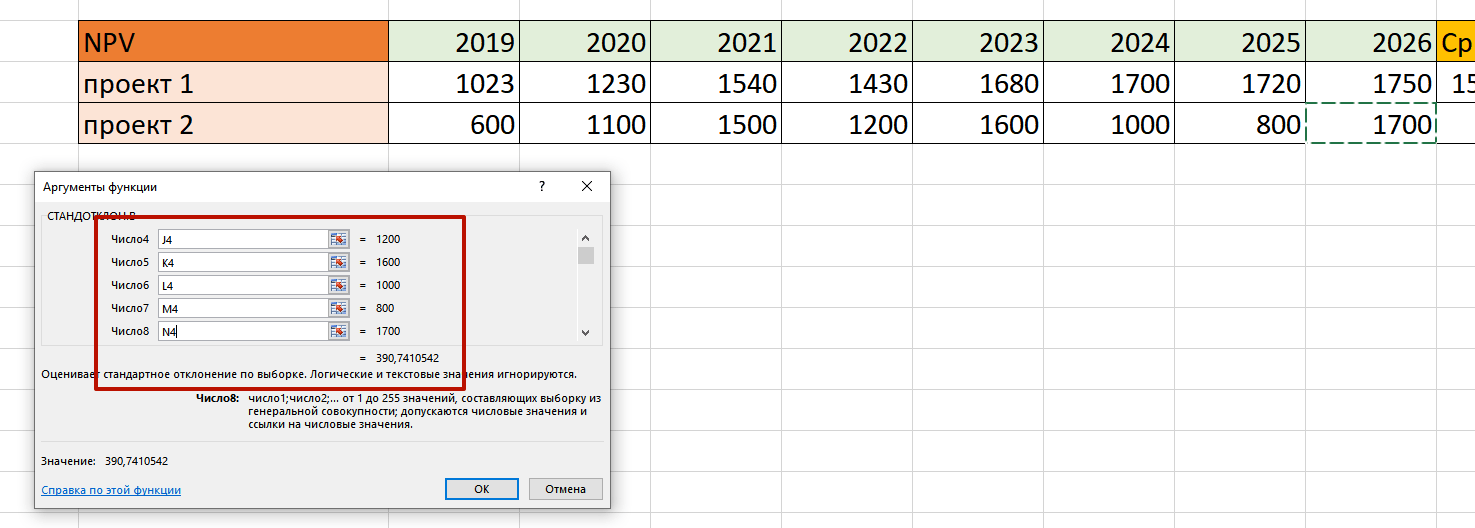
Теперь необходимо вычислить среднеквадратичное отклонение. Для этого предназначена функция СТАНДОТКЛОН.В

Обратите внимание, что в каждую строку необходимо вбить одну ячейку, а не выбирать весь диапазон:

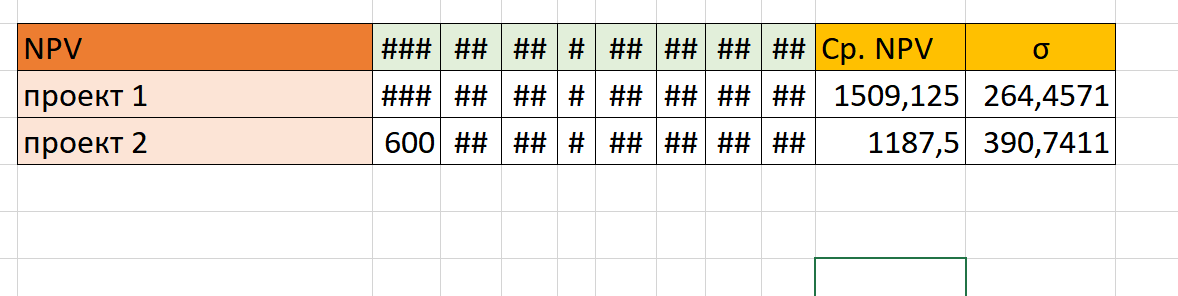
Таким образом, у нас есть рассчитанные средние значения доходности и среднеквадратичного отклонения по двум проектам:

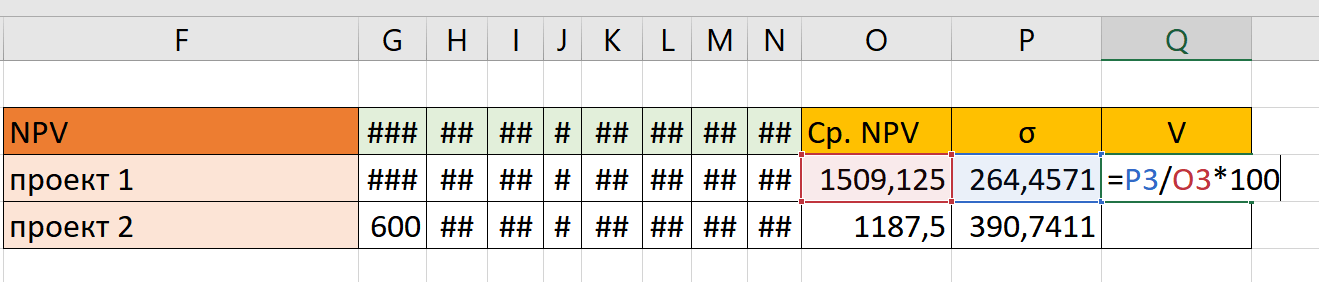
Теперь нам нужно найти коэффициент вариации. Для этого мы просто вписываем вручную формулу: ячейку σ делим на среднюю доходность и умножаем на 100:

Таким образом, получаем следующие значения коэффициента вариации:

Можно сделать вывод о том, что первый проект менее рисковый, чем второй.